いろいろ (1-x^2)y'' 2xy'=0 200241-X 2 1 y 2xy 2 0

Log(xy)=2xyOn differentiating both sides wrt x, we get( xy1 )(1 dxdy )=2(x dxdy y)⇒ dxdy = 2x 22xy−11−2xy−2y 2 at x=0,y=1 (from logxy=2xy)Now, at x=0,y′(0)= −11−2 =1 Ex 96, 14 For each of the differential equations given in Exercises 13 to 15 , find a particular solution satisfy the given condition 1 2 2 = 1 1 2 ; This problem has been solved!

Misc 7 Show That General Solution Is X Y 1 A 1 X Y 2xy

X 2 1 y 2xy 2 0

X 2 1 y 2xy 2 0-Answer to Solve the following (1 x^2)y"Steps for Completing the Square View solution steps Steps Using the Quadratic Formula = { x }^ { 2 } { y }^ { 2 } 2xy1=0 = x 2 y 2 − 2 x y − 1 = 0 All equations of the form ax^ {2}bxc=0 can be solved using the quadratic formula \frac {b±\sqrt {b^ {2}4ac}} {2a}

Solve The Following Differential Equation X2 Y2 Dx 2xy Dy 0 Given That Y 1 When X 1 Or Solve The Following Differential Equation If Y 1 When X 1 Mathematics Topperlearning Com 237hoo

Y(0) = –1 Want to see this answer and more?Multiply − 1 1 by − 2 2 y = 2 x y = 2 x y = 2 x y = 2 x y = 2x y = 2 x Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m x bY signo de prima para el primer (1) orden menos 2xy más 2xe en el grado x al cuadrado es igual a 0;

See the answerSee the answerSee the answerdone loading Solve by the Power Series Method (x^21)y"2xy'=0, y(0)=0 and y'(0)=0 Show transcribed image text Expert Answer Who are the experts?Dy/dx P(x)y=Q(x) We have y'2xy = 1 \ \ with \ \ y(0)=y_0 1 This is a First Order Ordinary Differential Equation in Standard Form So we compute and integrating factor, I, using; Solve differential equation \((1y^2xy^2)dx(x^2yy2xy)dy=0\) Your answer Email me at this address if my answer is selected or commented on Email me if my answer is selected or commented on

2xy9x^2 (2yx^21) (dy)/ (dx)=0, y (0)=3 \square!Experts are tested by Chegg as specialists in their subject areaExtended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music

2

4 A Solve The Differential Equation 1 X 2 Y 2xy L L 1 Y 0 Using Power Series Centered At 0 In Which Homeworklib

=0 when =1 (1 x2) 2xy = 1 1 2 Divide both sides by (1 2) 2 1 2 = 1 1Answer to Solve the differential equation (1x^2) y'' 2xy'= 0 given that one of the solutions is y_1(x) = 1 By signing up, you'll get for Teachers for Schools for Working Scholars® forFree PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystep

Solved The Differential Equation 1 X 2 Y 2xy V V Chegg Com

Use The Method Of Undetermined Coefficients To Solve 1 X2 Y 2xy 6y 0 Stumbling Robot

Show that the solution of differential equation y = 2(x^2 1) ce^(x^2) is dy/dx 2xy 4x^3 = 0 asked in Mathematics by Samantha ( 3k points) differential equationsThe normal line at any point should intersect the ellipse in two points It appears your function is x 2 2xy = 3y 2 This is not an ellipse, but a pair of lines that pass through the origin, at least according to what I got in my graphics application Differentitate this to get 2x 2x*dy/dx 2y = 6y*dy/dx so 2 (xy) = 2*dy/dx (3y x) andMedium View solution > View more CLASSES AND TRENDING CHAPTER class 5

For The Differential Equation X 2 Y 2 Dx 2xy Dy 0 Which Of The Following Are True A Solution Is X 2 Y 2 Cx B X 2 Y 2 Cx C X 2 Y 2 X C D Y 0 0

2

Question (x^2 1) y' 2xy^2 = 0, y(0) = 1 This problem has been solved!Trigonometry Graph x^2y^22x2y1=0 x2 − y2 − 2x − 2y − 1 = 0 x 2 y 2 2 x 2 y 1 = 0 Find the standard form of the hyperbola Tap for more steps Add 1 1 to both sides of the equation x 2 − y 2 − 2 x − 2 y = 1 x 2 y 2 2 x 2 y = 1 Complete the square for x 2 − 2 x x 2Answer (1 of 5) The equation \displaystyle{ (1x^2)y'' 2xy' 2y = 0 }\qquad(1) Since we have no obvious way to find any particular solution of (1) so we should try to find its general solution in the form of a power series as follows \displaystyle{ y = C_0 C_1x C_2x^2 \dots C_nx^2

Cbse 9 Math Cbse Polynomials Ncert Solutions

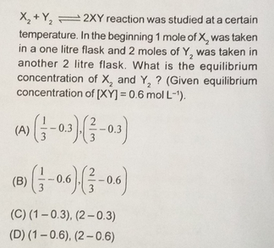
X2 Y2 2xy Reaction Was Studied At A Certain Temperature In Scholr

Identical expressions (one x^ two)y''2xy= zero (1 plus x squared )y two strokes of the second (2nd) order minus 2xy equally 0 (one plus x to the power of two)y two strokes of the second (2nd) order minus 2xy equally zero (1x2)y''2xy=0 (1x²)y''2xy=0 (1x to the power of 2)y(x^2 1) y' 2xy^2 = 0, y(0) = 1;Y' dos xy2xe^x^2= cero ;

Use The Method Of Undetermined Coefficients To Solve 1 X2 Y 2xy 6y 0 Stumbling Robot

Solve 1 X 2 Dy Dx 2xy 4x 2 0 Subject To The Initial Condition Y 0 0 Sarthaks Econnect Largest Online Education Community

Y'2xy2xe en el grado x en el grado 2=0;1 How do I separate the terms?Y signo de prima para el primer (1) orden menos dos xy más 2xe en el grado x al cuadrado es igual a cero ;

100以上 X Y2 Dx 2xy X2 1dy0 ただクールな画像

Solve The Following Differential Equation X 2 Y 2 Dx 2xy Dy 0 Given That Y 1 When X 1 Sarthaks Econnect Largest Online Education Community

JEE Main 15 The normal to the curve, x2 2xy 3y2 = 0 at (1,1) (A) Does not meet the curve again (B) Meets the curve again in the second quadraExercise 1 1 x dy − y x2 dx = 0 Exercise 2 2xy dy dx y2 −2x = 0 Exercise 3 2(y 1)exdx2(ex −2y)dy = 0 Theory Answers Integrals Tips Toc JJ II J I Back Section 2 Exercises 5 Exercise 4 (2xy 6x)dx(x2 4y3)dy = 0 Exercise 5 (8y −x2y) dy dx x−xy2 = 0Solution for X^2y^22xy=0 equation Simplifying X 2 1y 2 2xy = 0 Reorder the terms X 2 2xy 1y 2 = 0 Solving X 2 2xy 1y 2 = 0 Solving for variable 'X' Move all terms containing X to the left, all other terms to the right Add '2xy' to each side of the equation X 2 2xy 2xy 1y 2 = 0 2xy Combine like terms 2xy 2xy = 0 X 2 0 1y 2 = 0 2xy X 2 1y 2 = 0

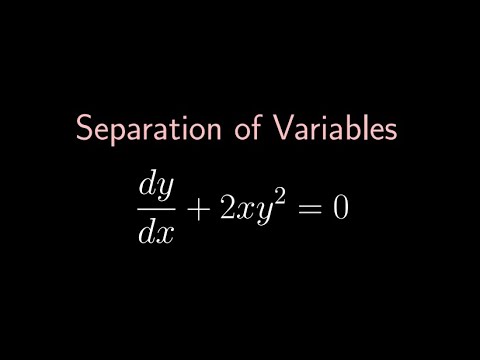
Separation Of Variables Dy Dx 2xy 2 0 Y 2xy 2 0 Youtube

Solve The Differential Equation Dy Dx 1 X Y2 Xy2 When Y 0 X 0 Studyrankersonline

$(2xy 3x^2) \, dx (x^2 y) \, dy = 0$ $M = 2xy 3x^2$ $N = x^2 y$ Test for exactness $\dfrac{\partial M}{\partial y} = 2x$ $\dfrac{\partial N}{\partial x} = 2x$Given the equation $$x^{2} 2 x y{\left(x \right)} \frac{d}{d x} y{\left(x \right)} y^{2}{\left(x \right)} = 0$$ Do replacement $$u{\left(x \right)} = \frac{y find a series solution about the point x=0 of (1x^2)y"2xy'2y=0

First Order Differential Equations Ppt Download

Show That The Equation 5x4 3x2y2 2xy3 Dx 2x3y 3xy2 5y4 Dy 0 Is An Exact Differential Equation Find Its Solution Mathematics 2 Question Answer Collection

This is not satisfactory since the expression 2y−1 2xy−e−2y depends on y We try µ= µ(y) Since the computations were not performed above, we do them fromExperts are waiting 24/7 to provide stepbystep solutions in as fast as 30 minutes!* How can I determine if the equation (2x3) (2y2)y' = 0 is exact or not?

Solve The Following Differential Equation 1 X 2 Dy Dx 2xy 1 1 X 2 Given Y 0 When X 1 Sarthaks Econnect Largest Online Education Community

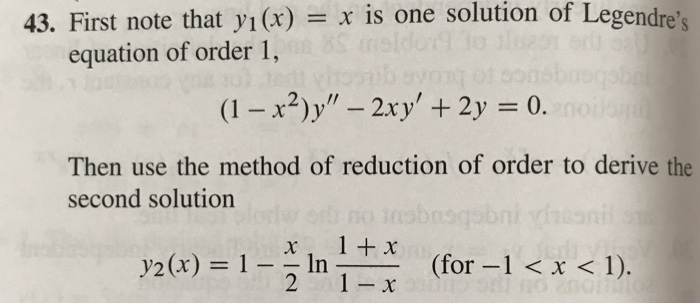
Solved 43 First Note That Yi X X Is One Solution Of Chegg Com

Weekly Subscription $249 USD per week until cancelled Monthly Subscription $799 USD per month until cancelled Annual Subscription $3499 USD per year until cancelledNow I know I need to take partial derivatives of certain terms of the equation, and call that M and N right?Click here👆to get an answer to your question ️ The solution of dy/dx = x^2 y^2 1/2xy satisfying y(1) = 1 is given by Consider the differential equation, y 2 d x (x − y 1 ) d y = 0 If value of y is 1 when x = 1, then the value of x for which y = 2, is?

Use The Method Of Undetermined Coefficients To Solve 1 X2 Y 2xy 6y 0 Stumbling Robot

Solved Consider The Following Equation X 2 1 Y 2xy Chegg Com

 y = (sqrt(pi/2)erf(x) y_0)e^(x^2) We can use an integrating factor when we have a First Order Linear nonhomogeneous Ordinary Differential Equation of the form;Solution for (3x2 – 2y²)y' = 2xy;Use separation of variables to solve the differential equation dy/dx 2xy^2 = 0 or equivalently written as y'2xy^2=0The steps to solving a DE by separation

Differential Equations

2

 Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeSolution for y^22xy=0 equation Simplifying y 2 2x 1y = 0 Reorder the terms 2x 1y y 2 = 0 Solving 2x 1y y 2 = 0 Solving for variable 'x' Move all terms containing x to the left, all other terms to the right Add 'y' to each side of the equation 2x 1y y y 2 = 0 y Combine like terms 1y y = 0 2x 0 y 2 = 0 y 2x y 2 = 0 y Remove the zero 2x y 2Combine all terms containing d \left (y2xyx\right)d=0 ( y − 2 x y x) d = 0 The equation is in standard form The equation is in standard form \left (yx2xy\right)d=0 ( y x − 2 x y) d = 0 Divide 0 by 2yxxy Divide 0 by − 2 y x x y

Misc 7 Show That General Solution Is X Y 1 A 1 X Y 2xy

2

Y 22y12xy=0, from which y 2 2(x1)y1=0, from which y=1x±√((x1) 21) by the quadratic formula or alternatively, y=1x±√(x 22x) Either way, you can pick any value of one variable that makes sense in the expression, to get the corresponding value(s) of the other variable in the solution;I = e^(int P(x) dx) \ \ = exp(int \2 How do I know which variable gets differentiated?

Legacy Www Math Harvard Edu

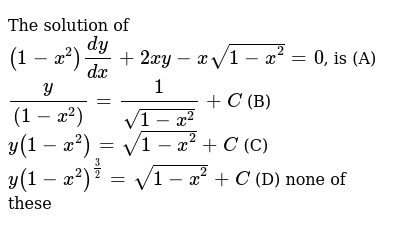
The Solution Of 1 X 2 Dy Dx 2xy Xsqrt 1 X 2 0 Is A Y 1 X 2 1 Sqrt 1 X 2 C B Y 1 X 2 Sqrt 1 X 2 C C Y 1 X 2 3 2 Sqrt 1 X 2 C D None Of These

See the answer See the answer See the answer done loading Show transcribed image text Expert Answer Who are the experts?Get an answer for '`y' (1x^2)y' 2xy = 0` Solve the differential equation' and find homework help for other Math questions at eNotesExperts are tested by Chegg as specialists in their subject area We review their content and use your feedback

1

1 X 2 Y 2xy 0 Reshit Differencialnoe Uravnenie

We identify M= 2xy−e−2y,N= y We compute M y = 1 6= 2 y= N x We seek such that (Mµ) y = (Nµ) x We try µ= µ(x) We obtain µ x = µ N x−M y N = µ 2y−1 2xy−e−2y;`x^2 y'' 2xy' 1 = 0` For a second order differential equation of the form y''=f(x,y'), the substitutions v=y' , v'=y'' lead to first order differential equation of the form v'=f(x,v)' and find X^{2} y^{2} 2xy1=0\\ 1 Ver respuesta Publicidad Publicidad brannd está esperando tu ayuda Añade tu respuesta y gana puntos campolit0 campolit0 Respuesta m Explicación paso a paso Publicidad Publicidad Nuevas preguntas de Matemáticas Cinco veces un número más 21 es igual a tres veces ese número menos 11 Calcula el número

Differential Equations Solved Examples Solve The Following Cauchy Euler Equation X 2y 5xy 5y 0

4 Y 3y 5y Y U The Differential Equation Of Family Of Curves R Y2 2ay 0 Where A Is Arbitrary Constant Is 1 X Y Y 2xy 2 2 X Y Y

 0 Office_Shredder said (xy) 2 = x 2 2xy y 2 >= 0 You know that already So x 2 xy y 2 >= xy If x and y are both positive, the result is trivial If x and y are both negative, the result is also trivial (in both cases, each term in the summation is positive) When one of x or y is negative, xy becomes positiveFor example , if I separate it so that its partial x (2x3) = 2 partial yFind the particular solution of the differential equation (1 y^2)(1 log x)dx 2xy dy = 0 given that y = 0 when x = 1 asked May 13 in Differential Equations by Rachi (

Solved Solve 1 X 2 Y 2xy 2y 0 Via Simple Chegg Com

Solve Bvm Problem D2y Dx2 Y 0 Y 0 1 H 1 4by Finite Nbsp Difference Method

 Assuming a power series solution like this #y = a_0 a_1 x a_2 x^2 a_3 x^3 ldots = sum_0^oo a_n x^n# #implies y^' = sum_1^oo n a_n x^(n1) qquad qquad y^('')= sum_2^oo n (n1)a_n x^(n2)#Graph x^2y^26x2y1=0 Subtract from both sides of the equation Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola Substitute the values of and into the formula Cancel the common factor of andSo conclude that y = 1− x2 4 x4 12 6 Solve the initialvalue problem y00 −2xy0 8y = 0, y(0) = 0, y0(0) = 1 (Notice that the differential equation is

3x 2y 2xy 1 X 2 Y 7 6 Brainly In

Ex 9 5 15 Class 12 Find Solution 2xy Y 2 2x 2 Dy Dx 0 When

∂I∂x = M(x, y) 0 − 2xy 0 g'(x) = 3x 2 − 2xy 2 −2xy g'(x) = 3x 2 − 2xy 2 g'(x) = 3x 2 2 And integration yields g(x) = x 3 2x C (equation 2) Now we can replace the g(x) in equation 2 in equation 1 I(x, y) = 2y 3 − x 2 y 3y x 3 2x C And the general solution is of the formI like the first one, because it means that$(1x^2)y''2xy'by =0 $ with $b = a(a1)$ When $x$ is small, this is $y''by = 0 $ which has solutions $y =u\sin(x\sqrt{b})v\cos(x\sqrt{b}) $ So, this seems like what the solutions look like Proceeding mechanically, let $y(x) =\sum_{n=0}^{\infty} a_nx^n =a_0a_1x\sum_{n=2}^{\infty} a_nx^n $ The reason for this will appear later

2

Differential Equations Solved Examples Show That Following Differential Equation Is Not Exact 3x 2y 4 2xy Dx 2x 3y 3 X 2 Dy 0 Then Find An Integrating Factor To Solve The Differential Equation

Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!2y = 0, y_1(x) = x By signing up, you'll get thousands of stepbystep solutions to yourF(x,y) = Z M dx = Z 2xy2 2ydx = x2y2 2xy g(y) And check to see that f y = N f y = 2x2y 2xg0(y) = 2x2y 2x In this case, g0(y) = 0, and we don't need to add g(y) The implicit solution x 2y 2xy = C 4 Problem 13 (2x−y)dx(2y −x)dy = 0 Check first M y = −1 = N x, so the DE is exact Now, f(x,y) = Z M dx = Z 2x−ydx = x2 −xy

Find A Series Solution About The Point X 0 Of 1 X 2 Y 2xy 2y 0 Youtube

For The Differential Equations Find The Particular Solution Satisfying The Given Condition 2xy Y 2 2x 2 Dy Dx 0 Y 2 When X 1 Mathematics Shaalaa Com

Steps for Completing the Square View solution steps Steps Using the Quadratic Formula (y1) { x }^ { 2 } 2xyy1=0 ( y − 1) x 2 − 2 x y y 1 = 0 All equations of the form ax^ {2}bxc=0 can be solved using the quadratic formula \frac {b±\sqrt {b^ {2}4ac}} {2a}Rewrite 2xy dxx2 dy−1 dy = 0 2 x y d x x 2 d y − 1 d y = 0 Change the sides $$2 xy \ dx x^2 \ dy = 1 \ See full answer belowAnswer (1 of 7) This answer uses an approach involving an integrating factor rather than separation of variables y'2xy=0 Note that the integrating factor, \mu, takes on the form of e raised to the integral of the coefficient in front of y In this example it is e^{\int 2x dx} \mu=e^{\int2

Givenof Solve The Equation 1 X 2 Y 2xy 2y 0 Giventhat Y X Is A Solution Brainly In

Solve The Following Ode S For Y X A X2y 2xy 2y 0 Y 1 2 Y 1 1 Homeworklib

Miscellaneous Problems Differential Equations

2

2

2

Solve The Following Differential Equation X2 Y2 Dx 2xy Dy 0 Given That Y 1 When X 1 Or Solve The Following Differential Equation If Y 1 When X 1 Mathematics Topperlearning Com 237hoo

Exact Non Differential Equation

Verifying Solutions To Differential Equations Video Khan Academy

Solve The Following Differential Equation X2 Y2 Dx 2xy Dy 0 Given That Y 1 When X 1 Or Solve The Following Differential Equation If Y 1 When X 1 Mathematics Topperlearning Com 237hoo

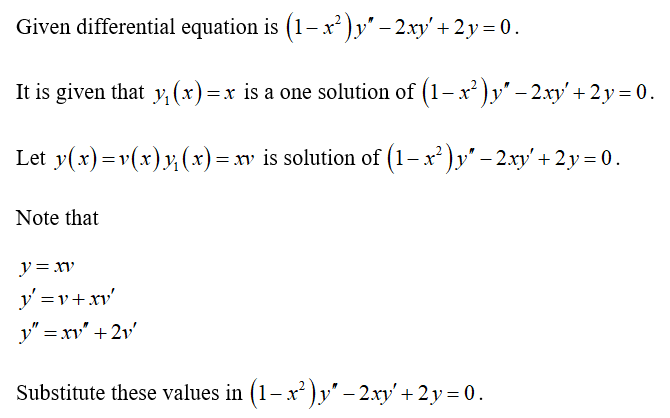
Answered First Note That Yi X X Is One Bartleby

Find Dy Dx If X 2 2xy Y 2 0 Brainly In

2

Chebyshevs Differential Equation Math Assignment Docsity

Ppt First Order Differential Equations Powerpoint Presentation Free Download Id

Solved Solve The Legendre Equation 1 X 2 Y 2xy N N Chegg Com

Y 2xy E X Dx E Xdy 0 Maths Questions

How To Solve Y 2xy 1 Dx Xdy 0 Quora

11 Equation Of The Parabola With Focus 3 4 And Dir Math

2

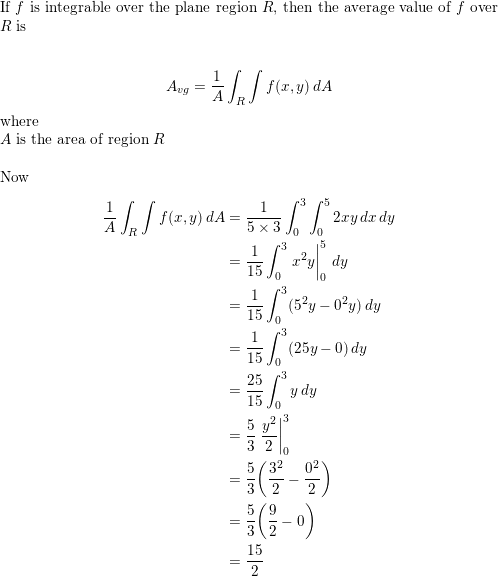
Find The Average Value Of F X Y Over The Plane Region R F X Y 2xy R Rectangle With Vertices 0 0 5 0 5 3 0 3 Homework Help And Answers Slader

Show Function F X Y X 2 Y 2 2xy Is 1 1 By Inverse Function Theorem Mathematics Stack Exchange

Iit 04 Find Y 0 If Y Is A Function Of X And Ln X Y 2xy 0 Youtube

Use The Reduction Of Order Method To Solve The Following Problem Given One Of The Solution Y1 A X 2 1 Y 39 39 2xy 39 2y 0 Y1 X B 2x 1 Y 39 39 4 X 1 Y 39 4y 0 Y1 E 2x C X

Solved Reduce To First Order And Solve 1 X2 Y 2xy Chegg Com

1

The Solution Of 1 X 2 Dy Dx 2xy 4x 2 0 Is Sarthaks Econnect Largest Online Education Community

How To Solve This Equation Math 2xy Y Dx X 2 X Dy 0 Math Quora

Solve The Following Differential Equations 1 X2 Y2 Dx 2xy Dy 3 Xly Dx 2 Y2 Dy 0 V T U 10 6 Y2 X2 Dx Xy Day Wegglab

Differential Equations Variation Of Parameters X 2y 2xy 2y X Ln X Youtube

Hw 4

Show That The General Solution Of The Differential Equation Dy Dx Y 2 Y 1 X 2 X 1 0 Is Given By X Y 1 A 1 X Y 2xy Where A Is Parameter Mathematics Shaalaa Com

Solve The Differential Equation Left 1 X 2 Right Frac Dy Dx 2xy 4 X 2 0 Subject To Initial Condition Yleft 0right 0 Snapsolve

If Y Tan 1x Show That 1 X2 Y 2xy 0 Maths Inverse Trigonometric Functions Meritnation Com

1a Engineering Mathematics Ppt Download

Polynomial Solution Of The Equation 1 X 2 Y 2xy 6y 0 Mathematics Stack Exchange

Solved Consider The Equation 1 X 2 Y 2xy 12y 0 Chegg Com

Ncert Exemplar Solutions For Class 12 Maths Chapter 9 Differential Equations Grab Pdf For Free

3 2 Problems Find General Solutions In Powers Of X Of The Diferential Equa Tions In Problems 1 T Homeworklib

Show That The General Solution Of The Differential Equation Dy Dx Y 2 Y 1 X 2 X 1 0 Is Given By X Y 1 A 1 X Y 2xy Where A Is Parameter Mathematics Shaalaa Com

Power Series

Second Solution For Reduction Of Order X 2 1 Y 2xy 2y X 2 1 Youtube

Find The Equation Of A Curve Passing Through Origin And Satisfying The Differential Equation 1 X 2dy Dx 2xy 4x2 Studyrankersonline

Solved Use The Method Of Frobenius To Obtain A Series Solution Of The Differential Equations I X 2y Xy X 2 K 2 Y 0 Ii 1 X 2 Y 2xy K K 1 Y

Elearningbothraclasses Com

Ex 9 6 8 Find General Solution 1 X2 Dy 2xy Dx Ex 9 6

Answered Reduce To First Order And Solve 1 Bartleby

Use The Method Of Undetermined Coefficients To Solve 1 X2 Y 2xy 12y 0 Stumbling Robot

2

Power Series Solution To Y 2xy 0 Mathematics Stack Exchange

2

Prove That U X 2 Y 2 2xy 2x 3y Is Harmonic And Find Harmonic Conjugate V Edurev Iit Jam Question

Implicit Differentiation

Power Series

Solved Solve The Following Differential Equations X Y 3 Dx X Y 1 Dy 0 2 X Y 1 Dx 3x 4y 2 Dy C 3 1 Y 2 Xy 2 Dx X 2y Y 2xy Dy Course Hero

Solved Assignment Use The Method Of Frobenius To Obtain A Series Solution Of The Differential Equations I X 2y Xy X 2 K 2 Y 0 Ii 1 X 2 Y 2xy K K 1 Y

The Differential Equation For The Family Of Curves X 2 Y 2 2ay 0 Where A Is An Arbitrary Constant Is A X 2 Y 2 Y 2xy B 2 X 2 Y 2 Y Xy C 2 X 2 Y 2 Y Xy D X 2 Y 2 Y 2xy

Solved Use The Properties Of Legendre Polynomials To Solve The Following Problems A Find The Solution Of 1 X 2 Y 2xy By F X Valid In Course Hero

Ex 9 6 14 Find Particular Solution 1 X2 Dy Dx 2xy

Ex 9 6 14 Find Particular Solution 1 X2 Dy Dx 2xy

X 2 Y 2 Dx 2xy Dy 0 The Solution To This Differential Equation Represents Which Curve

Assignment 1

What Is The Solution To The Differential Equation Math 1 X 2 Y 2xy 2y 0 Math Quora

Answered 7 Y 9 Xy Y Vx 11 Xy 2y X X 0 Bartleby

Solved Find The Power Series Solution Of The Differential Equation About An Ordinary Point X 0 1 X2y 2xy 2y 0 Why We Find Power Series Soluti Course Hero

Iith Ac In

Incoming Term: x 2 1 y 2xy 2 0,